AAO Exam-CT 15: Quant (Mensuration)

AAO Exam-CT 15- Quant (Mensuration)

0 8207

1. The area of a rectangle is thrice the area of a square. One side of the square is 4 cm, which is equal to the breadth of the rectangle. Find the length of the rectangle.

10
14
12
20
None of these

Solution

Given:

One side of the square is 4 cm = Breadth of the rectangle

The area of the rectangle is thrice the area of the square

Formula used:

Area of a square = side²

Area of a rectangle = (Length × Breadth)

Calculation:

So, the area of the square = 4² cm² = 16 cm²

According to the question, the area of the rectangle = (16 × 3) cm² = 48 cm²

As per the question, the breadth of the rectangle is 4 cm

So, the length = (48/4) cm = 12 cm

∴ The length of the rectangle is 12 cm.

2. The length and breadth of a rectangular wall are 30 metre and 24 metre respectively and the cost of painting the wall is Rs. 3,240. Find the rate of painting per square metre.

Rs. 4.2
Rs. 4.5
Rs. 4
Rs. 4.8
Rs. 4.4

Solution

Given:

Length of wall = 30 metre

and Breadth of wall = 24 metre

The total cost of painting = Rs. 3,240

Formula used:

Area of a rectangle = Length × Breadth

Calculation:

Let the rate of painting per square metre be Rs. x.

Then, (Area of the wall) × Rate = Total cost

⇒ 30 × 24 × x = Rs. 3,240

⇒ 720x = Rs. 3,240

⇒ x = Rs. 4.5

∴ The rate of painting per square metre is Rs. 4.5.

3. The radius of a sphere is equal to the radius of a cone and the volume of the sphere is equal to the volume of the cone. Find the curved surface area of the sphere when the height of the cone is 28 m. (Take π = 22/7)

612 m²
614 m²
616 m²
618 m²
620 m²

Solution

Given:

Radius of a sphere = Radius of a cone

Volume of the sphere = Volume of the cone

Height of cone = 28 m

Formula used:

(1) Volume of a sphere = (4/3)πr³

(2) Volume of a cone = (1/3)πr²h

(3) Curved surface area of a sphere = 4πr²

where, r = radius and h = height

Calculation:

Let the radius of the sphere be x cm.

Then, Volume of sphere = Volume of cone

⇒ (4/3)π(x)³ = (1/3)π(x)² × 28 cm

⇒ x = 28/4

⇒ x = 7 m

Now, Curved surface area of the sphere = 4πr²

⇒ 4 × (22/7) × 7²

⇒ 616 m²

∴ The curved surface area of the sphere is 616 m².

4. The area of the rectangle is 25% less than that of the area of the square. The radius of the largest possible circle inside the square is 20 cm. If the difference between the length and breadth of the rectangle is 10 cm, then, what is the perimeter of the rectangle?

140 cm
150 cm
160 cm
130 cm
None of these

5. The ratio of the sides of two equilateral triangles is 2 : 3. If the area of the smaller triangle is 360 cm², Find the area of the large triangle.

450 cm²
540 cm²
810 cm²
500 cm²
480 cm²

Solution

Given:

Area of smaller triangle = 360 cm²

a₁ : a₂ = 2 : 3

Concept Used:

Area of Equilateral triangle (A) = $\frac{\sqrt{3}}{4}$ a²

a = Side of Triangle

Calculation:

$\frac{A_{1}}{A_{2}}$ = $\frac{(a_{1})^{2}}{(a_{2})^{2}}$ = $\frac{4}{9}$

Here, 4 ≡ 360 cm²

⇒ 9 ≡ 360 × (9/4)

A₂ = 810 cm²

∴ Area of larger triangle is 810 cm².

6. The circumference of a circular garden is 22 cm and the area of a circular garden is 25% more than the perimeter of a square hall. Find the area of the square hall?

59.29 cm2
69.64 cm2
58.56 cm2
70.21 cm2
68.95 cm2

Solution

Given:

Circumference of Circle = 22 cm

Area of circular garden = 125% of the perimeter of a square

Concept Used:

Circumference of Circle = 2πR

Area of Circle = πR²

Perimeter of Square = 4a

a = Side of the Square

R = Radius of Cylinder

Calculation:

Circumference of Circle = 2πR

⇒ 2πR = 22

⇒ 2 × (22/7) × R = 22

Radius of circular garden = (22 × 7)/(2 × 22)

⇒ 7/2 cm

Area of circular garden (πR²) = (22/7) × (7/2) × (7/2)

⇒ 38.5 cm²

Perimeter of square = 38.5 × (4/5)

⇒ 4a = 38.5 × (4/5) cm

⇒ a = 7.7 cm

Area of square hall = 7.7 × 7.7

⇒ 59.29 cm²

∴ The area of square hall is 59.29 cm².

7. There are two right circular cylinders, the volume of first one is thrice of the volume of the second one. If the ratio of their height is 5 ∶ 2, find the ratio of their radii.

√6 ∶ √5
√5 ∶ √6
√3 ∶ √7
√2 ∶ √5
None of these

Solution

Given:

The volume of the first one is thrice of the volume of the second one

The ratio of their height is 5 ∶ 2

Formula used:

The volume of a right circular cylinder = πr²h

Calculation:

Let the height of the first one be 5h and the height of the second one be 2h and also their radii be r₁ and r₂ respectively.

The volume of the first one is thrice of the volume of the second

So, the volume of the first one = πr₁²(5h)

The volume of the second one = πr₂²(2h)

According to the question, πr₁²(5h) = 3 × πr₂²(2h)

⇒ (r₁)²/(r₂)² = (6/5)

⇒ (r₁)/(r₂) = (√6/√5)

⇒ r₁ ∶ r₂ = √6 ∶ √5

∴ The ratio of their radii is √6 ∶ √5.

8. Cuboid shape water tank having to measure 90 m x 40 m, 150 stones are thrown into it. If the average displacement of water by a stone is 8 m³, What will be the rise in water level of tank?

1/3 m
4 m
3 m
2/5 m
None of these

Solution

Given:

Length of tank = 90 m

Breadth of tank = 40 m

Formula:

Volume of cuboid = l × b × h

Calculations:

Given, Average displacement of water by a stone = 8 m³

Then, the total volume of water displaced by 150 stones = 150 × 8 m³ = 1200 m³

The total volume of the tank (Volume of the cuboid) = l × b × h

⇒ 90 × 40 × h

⇒ 3600 × h

here h is the height by which the water level rises

Now, Total volume of the tank = total volume of water displaced by 150 stones

⇒ 3600 × h = 1200

⇒ h = 12/36

⇒ h = 1/3 m

∴ The water level rises by 1/3 m

9. A right circular cone of radius 7 cm and height 15 cm is inscribed in a right circular cylinder of same radius and same height. What is the volume of remaining portion?

2110 cm3
2910 cm3
1015 cm3
1540 cm3
1758 cm3

Solution

Formula Used:

Volume of cylinder = πr2h

Volume of cone = (1/3)πr²h

where, r → Radius, h → Height

Calculations:

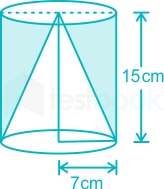
Radius of cone and cylinder = 7 cm

Height of cone and cylinder = 15 cm

Volume of remaining portion = Volume of cylinder - Volume of cone

⇒ Volume of remaining portion = πr2h - (1/3)πr2h = (2/3)πr2h

⇒ Volume of remaining portion = (2/3) × (22/7) × (7)² × 15

⇒ Volume of remaining portion = 1540 cm³

∴ The volume of remaining portion is 1540 cm³.

Shortcut Trick

Volume of remaining portion = (2/3)πr2h

⇒ Required volume must be a multiple of 11

Checking option (4),

1540/11 = 140

⇒ Volume of remaining portion = 1540 cm3

∴ The volume of remaining portion is 1540 cm3.

10. The base of a right prism is a regular hexagon of side 12 cm. If the height of the prism is 9√3 cm, then its volume is?

5848 cu.cm
5736 cu.cm
5832 cu.cm
5898 cu.cm
5558 cu.cm

Solution

Given:

Side of hexagon = 12 cm

Height of prism = 9√3 cm

Formula used:

Volume of prism = area of base × height

Area of hexagon = (3√3)/2 × side²

Calculation:

Area of base = (3√3)/2 × 12 × 12

⇒ 216√3 sq.cm

Volume = 216√3 × 9√3

⇒ 5832 cu.cm

∴ The volume is 5832 cu.cm

What is AAO Exam and How to pass AAO Exam?